3 Simple Steps to Find an Inverse Function

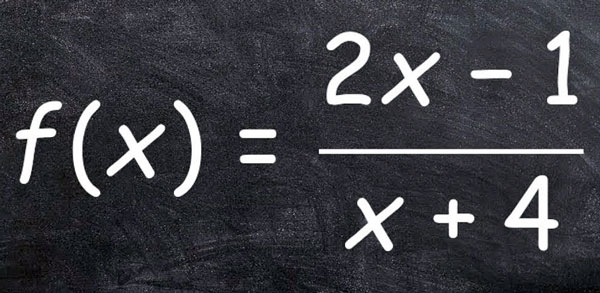
Inverse functions are used to cancel the effect of one function in mathematics, the inverse function is also known as the anti function and it is defined as “It is a function which can reverse the effect of another function”.

It is better for our convenience inverse function calculator to find the inverse of the function and to cancel out the effect of the function. Now if a function “f” is solved x with respect to y, then the inverse of the “f” is solved y with respect to the x.

Then we can find the reverse of the function and these two functions cancel out each other’s effect. The inverse function calculator can make the calculations simple for you, but you need to understand the concept in mathematics.

Now if the function is represented by “F” then the Inverse of the Function would be represented by “F-1” The (-1) is not the exponent of the function but it is the representation of the Inverse of the functions:

Why we use the inverse function:

The usage of the inverse function is enormous in the Mathematical calculations, as these are commonly used to undo the effect the other corresponding function, we can say the subtraction is inverse of the addition and the multiplication is inverse of the division, these all are cancelling the effect of each other.

Now think of the formula of the Farenheit and the Celsius scales, their values are inverse to each other and cancelling  the effect of each other we can use an inverse of a function calculator to find the inverse of function, the inverse function calculations are connected to every function in Mathematica, Now when we find the Logarithm the Inverse of it the Anti Logarithm.

 When we find the derivative the Inverse of it is Antiderivative which is also known as Integration. The same apply to the Trigonometric ratios, when we find the values of the sin, cos and the tan, then values of the sin-1,cos-1, and the tan-1 are also more than useful, if we want to reverse the calculation, you may think how find the inverse of a function calculator, this simple when we drive a function the inverse calculations automatically come into surface to inverse the calculation of the function.

Students may sometimes require instantaneous Inverse function calculations, so they can use the  inverse function calculator.

Characteristics an Inverse functions:

There are some of the characteristics of an Inverse function, one of them is that the Inverse function returns back the original function if we again calculate the output or the resultant.

This can be understood as using an inverse function calculator to find the inverse of a function, then again finding the solution of that inverse function we would ultimately find the original function from which we had started our calculations. You can use the inverse function calculator to do this for your fun and to find the important characteristics of the inverse function.

Now consider the two functions “f” and “g” which are inverse to each other, if we want to represent them the f(g(x))=g(f(x))=x. The Inverse function always fetches or returned beach the original values and return back the original function itself, if we solve it, this means the Inverse function is in the loop of the original function:

For example: f(x)=2x+5=y

Then g(y)=(y-5)/2=x, here is the inverse of the function f(x).

Now if we solve the function g(y)=(y-5)/2, then we again find the original function which is f(x)=2x+5, this shows the functions are inverse to each other and are canceling the effect of each other.

The 3 simple steps to find the Inverse of a function:

We can find the inverse of a function by using 3 simple steps, in the following example, we are converting a quadratic function to its inverse function in 3 simple steps:

Consider the following function we need to find the inverse of that function:

 f(x)=x3+5

Step 1:

■ In the first step, we need to replace the function  f(x) with “y”, to which we need to replace the function

f(x)=x3+5

y=x3+5  

Replace  f(x) by y

At this step we replace the f(x) by “y”, this would help to find the inverse of the function easily, and turn the values to another function “y”

Step 2:

■ In the second step, we are switching the roles of the x to y, we are interchanging their values to each other to reverse their role and the functionality of the given function. We have used the colored representation to reverse the whole reversal of their roles in the function.

■ y=x3+5 color code for x and y

■ x= y3+5  Interchange x and y 

■ x– 5= y3

Step 3:

■ At the final step, we are solving the “y” in terms of “x” to find its inverse function calculation.

■  Now we have replaced the function “y” with the  f-1(x), which is the final inverse of the function f(x)

■ 3x- 5=y

■ 3x– 5= f-1(x)

■ f-1(x)= 3x– 5————————(1)

Now taking cube root on both sides we get:

The final equation (1)    f-1(x)= 3x– 5 is the inverse of the function f(x)=x3+5, we used “3” steps to elaborate the inverse function calculations of the above-mentioned function. The inverse of function calculations is critical in finding the derivative and the antiderivative, trigonometric ratios, and inverse trigonometric ratios.

When we are finding a function, then it is necessary to find its inverse to reverse the calculation, we would find the original function if we are going to solve the inverse functions. We can use an inverse function calculator to find the inverse calculations of the function. Also, for more mathematical calculators, tap math calculators that will take you to another domain to resolve your math problems instantly and precisely.

Importance of the Inverse function:

For example when we find the values of a trigonometric ratio, for example, the values of sin60, then it is critical to find  sin-1 to convert the same values into sin60, same goes for Logarithm and for anti-Logarithm and for derivative and antiderivative.

Similar Stories